Definite Integrals!
Sounds scary doesn't it! It's actually pretty cool. SO...finding a definite integral means the same thing as finding the surface area of something. However, not every shape has an equation to find surface area like a cube (6a^2), sphere (4pi r^2), or a rectangular prism[box](2ab+2ac+bc) does. So to find the square footage of, let's say, an egg shaped room, we would have to use some other kind of method to find the area. Before the AMAZING invention of my handy-dandy TI-84 graphing calculator and the not-so-user-friendly AutoCADD, Reimann's Sum was just about the o
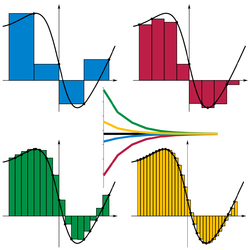nly way of finding an odd shape's area. Reimann's Sum is basically this: To find the approximate area under a curve, you chop that curve up into rectangulare pieces, find the area of each rectangle, and then add them all together (visual example to the right). OR...[(b-a)/n][f(x1)+f(x2)+f(x3)+f(x4)....+f(xn)]
where [a,b] are the limits on the graph, n is the number of times you are chopping up the curve, and f(x) is the area of each little rectangle.
I mean, I'll give it to Reimann, he came up with something very literal and something that you can make as approximate as you wanted, depending on how many times you chopped your curve up. What else are you gonna do when you don't have computers, right? BUT, the thing is that it just sucks and isn't completely accurate. The more accurate you want your answer to be, the more rectangular area's you're going to have to find, and that's not fun or fast! We have graphing calculators now, so let's use 'em!
So going back to our egg shaped room now! For almost every shape you could possibly make, there is a series of functions that when put together could form a shape very similar, if not exact, to the one you want. Now, I just finished taking a very simplified calculus class, so I'm not going to get into it like it does on Wiki, and I'll skip all of the lesson teaching on finding derivitives and integrating because you don't really need it for this. All you really need is a graphing calculator. So if you wanna play along with me, I'll include instructions. To enter functions for your calculator to graph, hit the y= button and enter in
y1=(x^2-5)/2
y2=-x^2+5
Now hit graph. You should see somewhat of an egg-shaped function. Now, first you must find the intersecting points of your 2 functions, so hit 2nd TRACE which will come up with a list of calculation options and hit 5:intersect, ENTER, ENTER, ENTER. The X value is 2.236068, which means the opposite intersection will be the same number except negative (these are your "limits.) Now, to find the surface area for the area under the first curve (y1) hit 2nd TRACE, 7: ~f(x)dx. It will say "Lower Limit?" and enter in -2.236068 ENTER, and "Upper Limit?" is 2.236068 ENTER. I will find the surface area above the first curve until 0, which is 7.45356 (the negative does not matter, since there is no such thing as negative surface area.) Now we need to find the surface area of the top of the egg, so repeat the above steps with only the y2 equation graphed (your limit of -+2.236068 is the same). You should end up with 14.904401. Now add the area from the top and bottom of the egg...
7.45356+14.9044
01=22.357961And there you have it! Lol, it sounds and looks confusing but really isn't once you learn all the cool stuff a TI-84 can do. But this way, an architect can know the EXACT square footage of an odd shaped room (not that there are very many odd shaped rooms that don't have angles, but just in case there were!). So if I were ordering hardwood for this floor I would order 23 square feet (wow that's a tiny egg-shaped room!)to minimize my cost, increase revenue, and use less resources. Of course, it can get way more complicated like finding volume by definite integrals, as the picture illistrates on the left, but I don't know how to do that.......YET!
Oh how fun calculus can be!
No comments:
Post a Comment